航空發動機輪盤部件一旦失效必將導致飛行器災難性事故 [1-2],是發動機安全性水平要求最高的部件 (失效概率 < 10-8 次 / 飛行小時)[3-6]。其中,鈦合金是發動機壓氣機輪盤的重要材料。銑削工藝經常是加工輪盤成品前的最后一步工序,直接影響著輪盤的表面完整性 [7],包括表面殘余應力、表面粗糙度等。加工引入粗糙度會在輪盤表面造成局部的應力集中,影響裂紋萌生;加工引入的拉伸殘余應力可降低疲勞壽命、壓縮殘余應力可提高壽命 40% 以上 [8-14],進而對輪盤的失效風險產生影響。因此,銑削加工工藝對表面殘余應力的影響規律是輪盤的安全性分析的重要輸入 [15]。
銑削形成的表面殘余應力受材料特性、切削參數、刀具參數、摩擦及傳熱等因素影響,獲取加工殘余應力的研究方法包括試驗方法、解析法及有限元法。傳統銑削殘余應力研究采用試驗方式,獲得銑削工藝參數對殘余應力影響的經驗公式,但效率低、成本高、且經驗公式可推廣性具有局限性 [16-17]。對于切削解析法,20 世紀 40 年代 Merchant 提出單一剪切面模型 [18]。此后,Shaw 等人引入材料非均勻影響,優化切削模型 [19]。Lee 和 Shaffer 引入滑移線場理論,建立理想剛塑性材料切削滑移線場模型 [20]。Oxley 在單一剪切面模型上進行修正,引入加工硬化、應變效應等因素,結合平面應變塑性理論,建立了平行面剪切區切削模型 [21-23]。
20 世紀 70 年代,美國伊利諾斯大學的 Klameck [24] 首次將有限元方法用于金屬切削領域,并對金屬切屑形成機理進行研究。1982 年 Usui 和 Shirakashi [25] 基于刀面切屑形狀及流線假設,建立了穩態正交切削模型,并預測切削應力、應變和溫度。Iwata [26] 采用剛塑性有限元模型,獲取切屑厚度、切屑卷曲度、切屑與刀具接觸長度,以及在平面應變正交切削中應變速率、應力和等效應變的分布;并建立了切屑和工件斷裂的韌性斷裂準則。然而上述研究沒有考慮彈性變形,因此無法獲得由于彈塑性變形不均勻引入的加工殘余應力。此后,Strenkowski 和 lcarroll [27] 將材料假設為熱彈塑性材料,采用等效塑性應變作為分離準則,獲取表面殘余應力分布。Shih [28] 提出了正交金屬切削過程的大應變有限元模擬方法、建立了粘滑摩擦模型,給出了在工件和切屑內部的主變形區和二次變形區法向應力和剪應力的分布,并成功基于有限元法獲取殘余應力,對準確預測殘余應力具有重要意義。Sasaharaa 等人 [29] 采用有限元方法模擬了從粗加工到精加工的切削順序對被加工層內力學特性的影響,結論表明隨著精加工次數增加,變形層和影響層逐步減小。
針對銑削仿真,包括三維切削仿真及二維簡化仿真。現有基于有限元法的三維切削仿真模型中,銑刀的復雜三維結構導致網格生成和重畫分耗費大量的資源。銑削二維簡化方式主要有以下三類。第一類是通過將變厚度的切削層簡化為等效厚度后進行正交切削仿真,包括等效均勻厚度切削模型 [30]、等效斜面工件切削模型 [31]、等效刀具斜向切削模型 [31]。第一類方式沒有考慮到銑削過程是一種間歇多次切削的過程,也沒有考慮到銑刀螺旋角對切削的影響,該方法無法獲得已加工表面的殘余應力。第二類是取平行于進給方向的銑刀主剖面來進行二維銑削仿真,該方法考慮了銑削的變厚度連續銑削,可以獲得已加工表面殘余應力,但第二類方法忽略了螺旋角的影響,實際銑削過程中,螺旋角會影響切削熱和切削力,也會影響切屑 [32-33]。第三類是通過等效平面的方式將螺旋角考慮到二維銑削仿真中 [34]。另外,將銑削簡化為單次銑削僅僅可以獲得銑削過程中的切削力和切削熱,無法獲得銑削后準確的已加工表面殘余應力的大小及分布情況。
綜上,傳統獲取加工殘余應力方法為試驗方法,然而耗時長、周期長、分散性高。解析法通過對切削力和切削熱單獨進行計算,并將機械應力與熱應力進行疊加,難以考慮機械載荷與熱載耦合交互作用的影響,且求解過程復雜。基于有限元法的切削仿真模型可獲取銑削殘余應力,然而對于三維銑削而言,銑刀的復雜三維結構導致網生成和重畫分導致仿真方案迭代周期長;而二維模型的技術較為成熟,且網格數量遠小于三維模型,計算量也遠小于三維仿真,但對于模型過度簡化。
對此,本文提出了考慮螺旋角的二維連續銑削簡化模型,采用二維有限元模型進行銑削加工仿真分析,獲取加工過程中切削力、切削溫度和材料應變等各種參數的變化規律,對系統地分析和研究切削機理和表面殘余應力具有重要的指導作用,從而為定量化分析制造加工對輪盤安全性的影響提供殘余應力參數輸入。
1、考慮螺旋角的銑削仿真模型
1.1 考慮螺旋角的二維連續銑削簡化模型
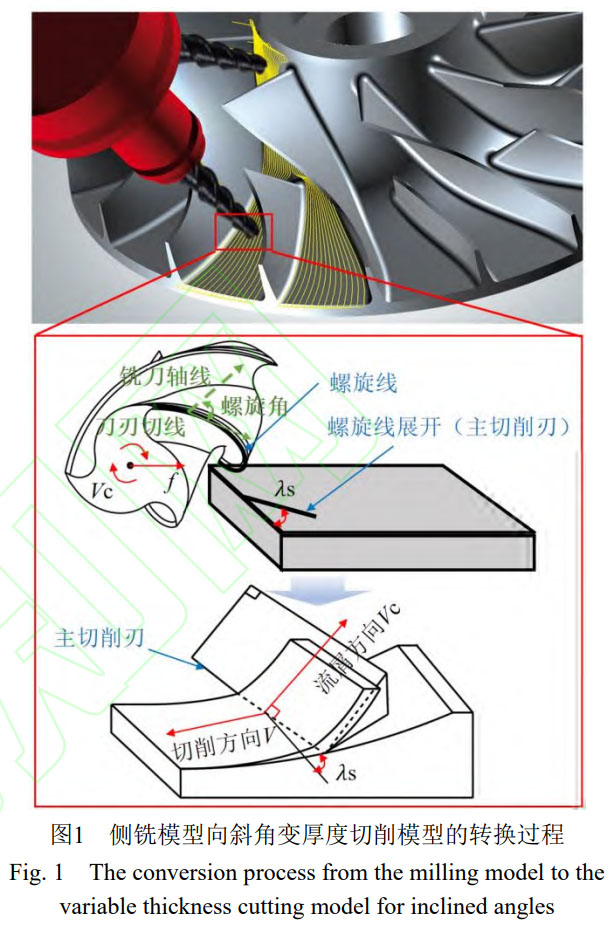
為獲得較為準確的已加工表面殘余應力,并能更真實地反映銑削加工的特性 —— 變厚度切削、斜角切削、周期性 (切削 - 卸載冷卻 - 切削) 間歇切削特性,本節提出考慮螺旋角的二維連續銑削簡化模型,即在銑削建模中考慮因螺旋角的影響導致的刀具參數的改變,并建立連續的多齒變厚度切削模型。
在采用等效平面的基礎上,用等效后的刀具參數建立二維連續多齒變厚度銑削仿真模型。
如圖1,螺旋銑刀刀刃沿進給方向的運動本質上是個斜角變厚度銑削的過程,即螺旋角等效為斜角切削中的刃傾角λs。由于銑削刀刃接觸工件的長度在毫米量級,銑削深度ae為 0.1mm,刀刃長度與銑削深度比值大于 5,因此采用平面應變假設,將三維模型簡化為平面正交切削模型 [35-37]。
在二維仿真模型中,主要參與切削并起重要作用的參數有刀具前角γ、刀具后角α及刃口鈍圓半徑rn。可基于刀具與切屑、工件間的真實作用機理,通過由法剖面、主剖面、前刀面、等效平面構成的四個坐標系之間的轉換關系 [37][圖 2 此處為原文圖片:斜角切削等效示意圖]。具體而言,YAr軸為前刀面主切削刃的法線方向,XAr軸與主切削刃重合,ZAr 軸垂直于前刀面,O-XArYArZAr 為由前刀面及前刀面法向組成的坐標系;Z1和Z2軸為主切削速度方向,切削主剖面為Y1OZ1,主剖面及主剖面法線組成坐標系 o - X1Y1Z1;Y2軸為等效平面與基線的交線,Y2OZ2平面為等效平面,等效平面及等效平面法線方向組成坐標系O-X2Y2Z2。
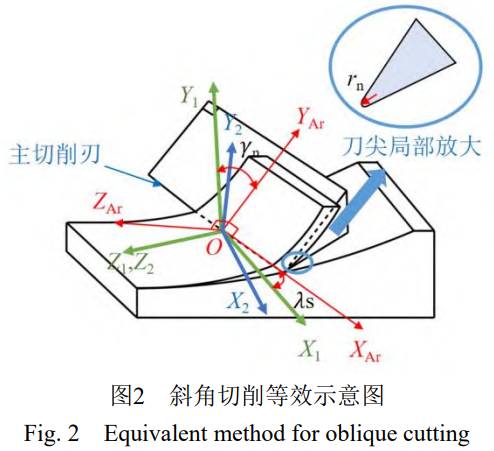
根據等效平面的定義總結推導出二維斜角切削仿真模型中刀具等效參數的函數關系式。
等效后刀具參數具體可由如下公式計算:
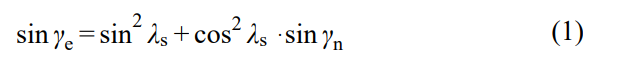
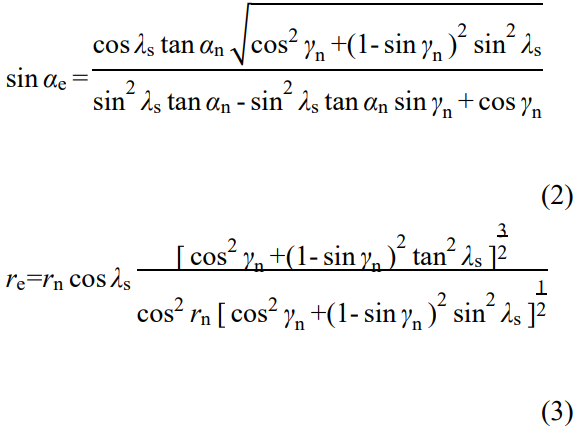
其中,γe為等效前角 (°);αe為等效后角 (°);re為等效鈍圓半徑 (mm);γn為法前角 (°);αn為法向后角 (°);rn為法剖面上的鈍圓半徑 (mm);λs為刃傾角 (°)。
上述公式(1)~(3)中用到的參數為法剖面上參數,而通過刀具制造商或者測量所獲取的參數一般為主剖面上的刀具參數,因此法剖面上的刀具參數需通過基本換算關系式(4)、(5)獲取:

其中,γ0為主剖面上的實測前角(°);α0為主剖面上的實測后角(°)。
1.2 關鍵準則
1.2.1 本構模型
本構模型描述流動應力與應變、應變率和溫度之間的相互作用關系。Johnson-Cook 模型將影響流動應力的應變硬化效應、應變率效應與溫度效應聯系在一起 [38],其表達式為:
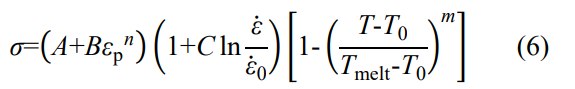
式中,A 為準靜態條件下的屈服強度;B 為應變εp為等效塑性應變;n 為硬化指數;C 為應變率強化參數;ε為等效塑性應變率;ε?0為參考應變率;T0為室溫;Tmelt為材料熔點;m 為熱軟化參數。
本文以鈦合金 Ti6Al4V 為研究材料,其 Johnson-Cook 本構模型參數 [39] 如表 1。
表 1 鈦合金 Ti6Al4V 的 Johnson-Cook 本構模型參數 [39]
| A/ MPa | B/ MPa | C | m | n | Tmelt /℃ | T0 /℃ |
| 843.8 | 785.6 | 0.033 | 0.841 | 0.26 | 1725 | 25 |
1.2.2 斷裂準則
金屬切削是材料在大應變和高應變率條件下不斷發生分離的過程,因此需要確定斷裂準則。材料分離斷裂準則可能受到多種因素的影響,例如平均應力、等效應力或者最大主應力。常用準則包括 Rice and Tracey 準則 [40],Cockcroft and Latham 準則 [41],Normalized Cockcroft and Latham 準則 [42],Oyane 準則 [43] 等,可以描述切削材料是否發生分離。需要注意的是,每個準則模型都有自己的一套假設、參數和函數形式,模型的選擇取決于材料特性、載荷條件以及可用的材料數據。
本文采用 Normalized Cockcroft and Latham 準則,這也是鈦合金切削常用的斷裂準則,是歸一化的 Cockcroft and Latham 方法 [44-45],假設最大主應力是引發斷裂的參數,
表示為:

其中,D 為材料的臨界斷裂值,也是分離系數;σ*為最大主應力;σ-為材料的等效應力;ε-?為等效應變。D 是歸一化參數,因此取值在 0~1 之間。本文取 0.1,認為隨著切削溫度升高,當最大主應力降低至常溫下最大主應力的 0.1 時,即發生斷裂 [46]。
1.2.3 摩擦模型
切削加工過程主要包含有兩個摩擦區,一個是前刀面與切屑的摩擦,另一個是后刀面與工件表面的摩擦,這兩個過程中的摩擦應力一般都是不均勻的。在滑移區,摩擦力小于極限剪切應力,屬于外摩擦力,其摩擦行為符合庫倫 (Coulomb) 摩擦定律。在粘結區,刀具和切屑接觸表面不發生相對滑動,摩擦力屬于內摩擦,屬于內部金屬剪切而引起的摩擦,剪應力是固定的,等于材料的屈服應力,此區域摩擦力等于極限摩擦剪切應力τmax。本文選擇庫倫摩擦模型,其摩擦行為可以用下式來表示:

式中,τf為摩擦力,μ 為滑移摩擦因數取0.25[47],τmax為材料的極限剪切流動應力,σn是工件與模具的正應力。
1.3 二維銑削殘余應力有限元仿真模型
1.3.1 基本假設
本文基于以下的條件對模型進行平面應變假設 [35-37],建立鈦合金銑削有限元仿真模型:
①切削寬度至少為切削深度的 5 倍;
②被加工工件為各向同性;
③忽略加工過程中相變;
④刀具為剛體。
1.3.2 刀具和工件幾何模型的建立
本文采用 DEFORM 軟件開展銑削仿真。在建模軟件 UG 中建立刀具幾何模型,將通過 1.1 節方法簡化等效后的刀具參數代入并建立二維模型,然后導入 DEFORM 有限元軟件中。
本文根據某廠實際生產鈦合金離心壓氣機轉子過程中精銑所用到的刀具 (刀具型號 SANDVIK SM50.1-0282-1038781620),采用光學三維測量儀測量刀具參數。首先將被測刀具固定在儀器的夾具上,調整焦距燈光等參數,以得到被測刀刃部分最清晰的成像,檢測現場如圖 3 a 所示 [圖 3 此處為原文圖片:銑削刀具角度測量試驗臺及刀具角度示意圖]。掃描出刀刃的三維輪廓后,構造垂直于刀刃的剖面 (圖 3 b),獲得剖面內的刀刃剖面的輪廓線,然后選擇高斯擬合來擬合輪廓,使擬合圓與刀刃處的輪廓線重合,從而獲得刀具的前角γ、后角α及刃口鈍圓rn。最終測量所得刃口鈍圓尺寸rn為 5.605μm,前角 19.292°,后角 15.963°。

為此,本文根據試驗所得刀具參數設置仿真算例。具體而言,采用直徑為 3mm 的三刃硬質合金立銑刀,前角 18.5°,后角 15.2°,螺旋角 45°,刃口鈍圓半徑尺寸rn為 5μm。根據 1.1 節方法計算等效刀具角度,等效前角為 34°,等效后角為 15.25°,等效前后可以忽略。
圖4為刀具與工件的空間相對位置。本文分析的工件尺寸為12mm×2mm。銑削方式為順銑。仿真模型設置的切削參數為:銑削深度ae=0.1mm;銑削主軸轉速Vc=2000~4000r/min;進給速度f=240mm/min,可結合銑削主軸轉速推算每齒進給量fr(mm/r):

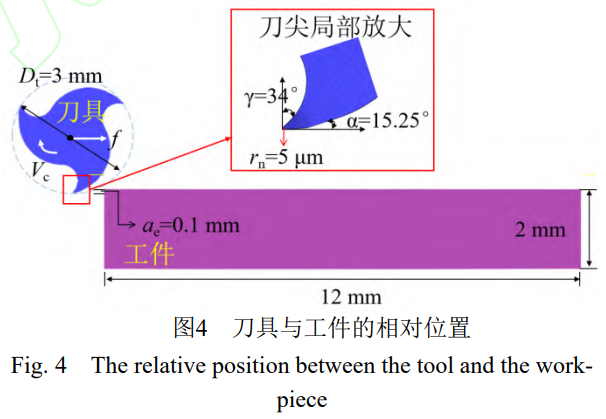
采用絕對數量、相對比例的網格劃分方式對工件和刀具進行網格劃分,并通過使用 DEFORM 中的網格局部細化窗口功能對工件上端 0.18mm 切削層以及刀具的刃口部分進行局部細化,如 [圖 5 此處為原文圖片:工件與銑刀網格局部細化] 所示。根據正交切削網格無關性分析可知,當工件和刀具局部接觸區域網格尺寸為 3μm 時,其殘余應力計算結果收斂 [48]。工件網格數為 27000 左右,切削層網格大小為 3μm;刀具網格數為 5000 左右,刃尖部分網格大小為 2μm。
1.3.3 邊界條件
銑削加工過程是刀具從工件上切除材料的材料去除成形方法,在刀尖和工件區域會發生高溫度、高應變、高應變率的熱力耦合過程。在進行銑削仿真分析時,針對刀尖與工件接觸局部區域進行建模。因此,從實際銑削過程簡化出刀尖工件二維正交切削模型時,需注意簡化模型的邊界為金屬材料。具體而言,S1、S2 面為換熱邊界條件,與空氣接觸;S3、S4 面為與金屬材料接觸的邊界,并且與切削局部區域相距較遠,設置為恒溫邊界,如 [圖 6 此處為原文圖片:銑削仿真邊界條件 (速度?位移?溫度和換熱)] 所示。設置環境溫度 20℃,工件和刀具的初始溫度為 20℃。空氣對流換熱系數 0.02N/(sec?mm?K),接觸區傳熱系數 40N/(sec?mm?K)。工件與環境換熱邊界為會與銑刀發生接觸的左邊界和上邊界,而右邊界和下邊界假設距離切削區足夠遠,其邊界溫度將不受切削區影響,因此將其設置為恒溫 20℃;銑刀換熱邊界為所有表面。

2、銑削表面殘余應力分析
2.1 加工表面殘余應力模擬步驟
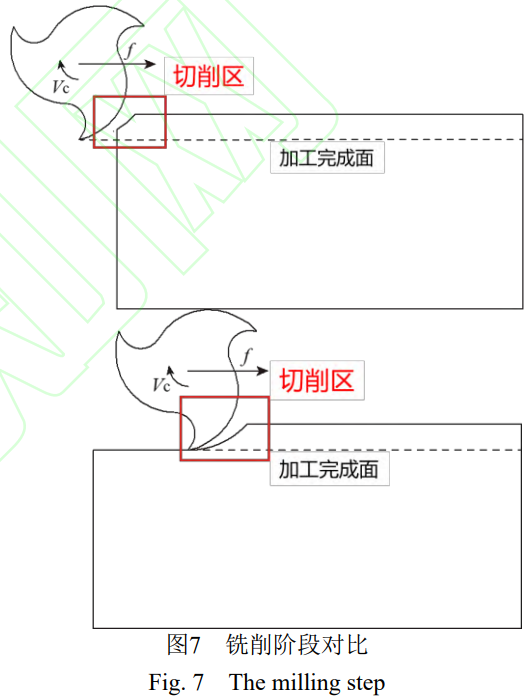
銑削過程是一個變厚度的間歇切削的過程,每個齒對工件進行周期性的切削,切屑由厚變薄的過程 (逆銑則相反)。銑削過程中,銑刀的運動由自轉和平動組成,在加工出完成面前,隨著切削的進行,每次切削的厚度會逐漸增大,直到加工出完成面后,切削厚度將保持一致,如 [圖 7 此處為原文圖片:銑削階段對比] 所示。由此判斷,銑削過程必存在切削過渡區和切削穩定區,一般的加工過程中,切削穩定區占主要地位,最能代表整個加工表面的加工質量。
結合實際的加工過程將已加工表面殘余應力的仿真模擬分為以下三個步驟,切削力加載階段;退刀階段;去約束冷卻階段。這一系列過程均在 DEFORM-2D 中完成。
2.2 銑削穩定區殘余應力的獲取
通過有限元仿真分析,得到銑削過程不同時刻的殘余應力分布情況,如 圖 8 所示。
可以看出,工件經歷一系列的卸載去約束冷卻后,表面殘余應力分布會進一步的發生改變。
銑削加工后表層殘余應力的三個重要特征參數為:
①表面殘余壓應力大小;
②最大殘余壓應力深度;
③殘余應力層深度。
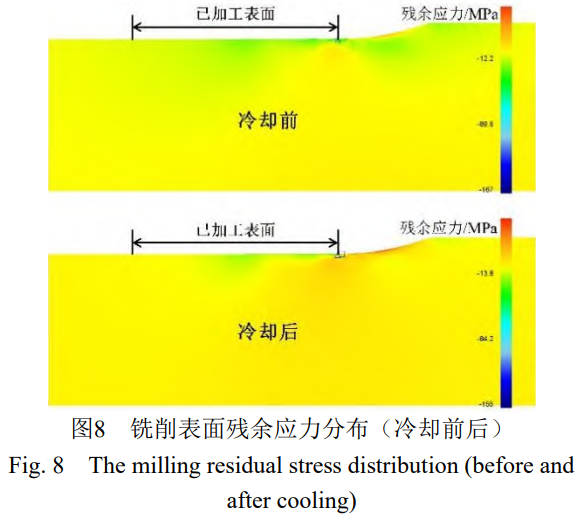
銑削完成后,排除切削區及自由邊界影響,在工件已加工表面切削穩定區域建立路徑,如 圖 9 所示。按照路徑在 DEFORM 后處理中提取 X 方向的殘余應力值,得到工件沿已加工表面深度方向上的殘余應力分布曲線如 圖 10 所示。從仿真結果可以看出,進給方向 (X) 的表面殘余應力呈現為壓應力,并在彈性卸載、熱應變釋放等過程后減小。冷卻后,最大殘余應力在表面達到 - 56MPa 左右并沿深度方向呈遞減趨勢至 0MPa 左右。
X 方向上工件已加工表面的殘余應力為殘余壓應力,此時在銑削加工過程中受 “擠光效應” 和 “塑性凸出效應” 及熱效應的影響。“擠光效應” 主導著機械應力引起的殘余壓應力占主要地位。隨著層深的增加殘余壓應力減小。

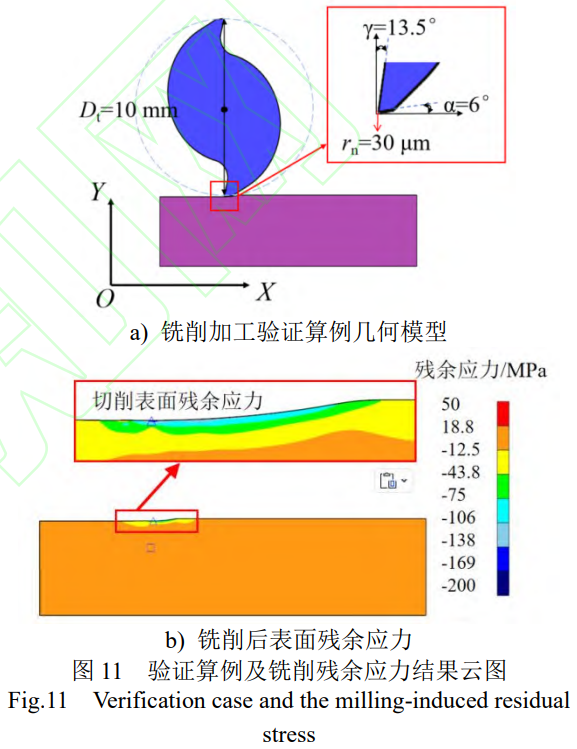
2.3 銑削仿真結果驗證
參考哈爾濱理工大學[39]開展的鈦合金銑削試驗:刀具為2刃立銑刀,直徑10mm,螺旋角為25°,前角為13.5°,后角為6°,刀刃鈍圓為30μm;工件材料為Ti6Al4V;主軸轉速Vc為600r/min,進給速度f為120mm/min,銑削深度ae為0.1mm,銑削方式為順銑,加工過程無冷卻液,如圖11所示。在上述試驗參數下,仿真所得工件加工表面X方向殘余應力為-132.27MPa,試驗測得表層殘余應力為-180MPa,試驗測得殘余應力峰值為-208,誤差26.66%。
2.4 銑削參數對殘余應力影響規律分析
影響銑削加工效果的主要有主軸轉速Vc、進給量f和刀具參數。本研究中刀具參數主要研究和其鋒利程度相關的前角γ和后角α。由于銑削過程是單齒間歇切削的過程,實質上影響銑削過程切削的就是影響每齒單次切削的參數。因此,本文進給量指每轉進給量fr。
根據鈦合金實際銑削加工參數推薦范圍制定仿真方案。為了探究銑削參數對殘余應力的影響規律,仿真方案涉及采用控制變量法,如表2所示。其中,刀具螺旋角均為45°,直徑為3mm,刀具前角γ=18.5°,后角α=15°,等效前角為34.0°,等效后角為15.2°。
表 2 銑削仿真方案
| 序號 | 變量 | 主軸轉速 (r/min) | 每齒進給量 (mm/r) | 銑削深度 (mm) |
| 1 | - | 2000 | 0.12 | 0.1 |
| 2 | - | 2500 | 0.12 | 0.1 |
| 3 | - | 3500 | 0.12 | 0.1 |
| 4 | - | 4000 | 0.12 | 0.1 |
| 5 | - | 2000 | 0.10 | 0.1 |
| 6 | - | 2000 | 0.18 | 0.1 |
| 7 | - | 2000 | 0.24 | 0.1 |
2.4.1 銑削主軸轉速對表面殘余應力的影響
對主軸轉速影響的表面殘余應力作出進一步研究,在銑削深度ae=0.1mm,每齒進給量fr=0.12mm/r,主軸轉速Vc分別取2000r/min、2500r/min、3500r/min、4000r/min的條件下,顯示了表面殘余應力隨主軸轉速的變化規律,如圖12。
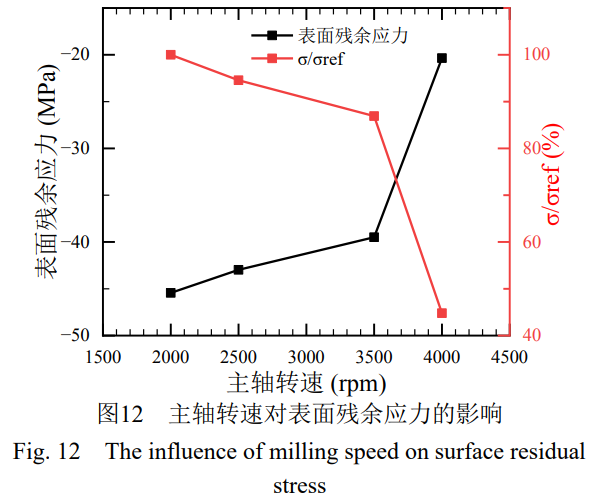
隨主軸轉速增大,殘余壓應力絕對值逐漸減小,表面殘余應力有向拉應力轉化的趨勢。其主要原因為主軸轉速增加時,刀具每齒單次切削速度變快,切削溫度隨之升高,切削熱增加,因此熱效應引起的殘余拉應力占主要地位,表面殘余應力隨著主軸轉速的增加逐漸向拉應力轉換。
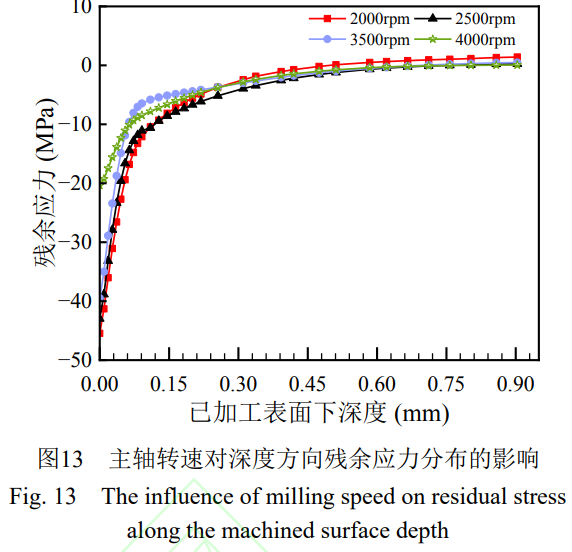
由 圖 13 可以看出,工件表面層為殘余壓應力,沿著深度方向 0~0.1mm 的厚度范圍內,殘余壓應力絕對值迅速減小,然后過渡為拉應力,拉應力始終處于一個較小的數值附近,最后接近于零。從圖上看,主軸轉速對殘余應力層深度的影響可以忽略,這是因為鈦合金的導熱系數低,短時間內溫度的升高無法傳導到里層。因此,主軸轉速對殘余應力層厚度影響很小。
2.4.2 銑削進給量對表面殘余應力的影響
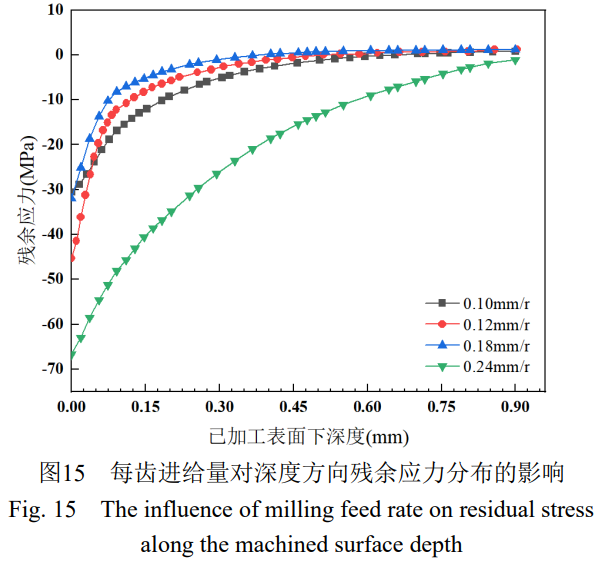
在銑削深度ae=0.1mm,主軸轉速Vc=2000r/min,每齒進給量fr分別取0.10mm/r、0.12mm/r、0.18mm/r、0.24mm/r。圖14及圖15顯示了表面殘余應力隨每轉進給量的變化規律。
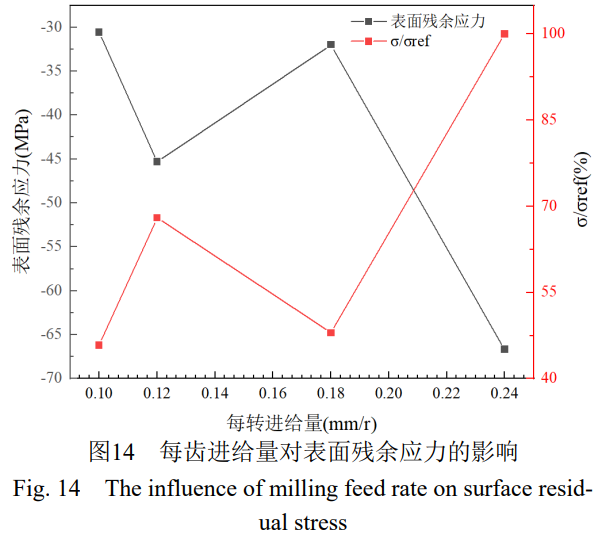
可以發現每齒進給量在0.10~0.18mm/r范圍內時,表面殘余壓應力均處于-30~-45MPa,當每齒進給量繼續增加,表面殘余壓應力增大,約為-67MPa。這是因為殘余應力主要受機械載荷和熱載荷的共同作用,機械載荷主要引起“擠光效應”,產生殘余壓應力,而熱應力引起殘余拉應力。在較高的進給量情況下,材料去除增快,機械載荷引起的殘余應力起主導作用,此時增大進給量,“擠光效應”增強,工件表面層壓應力增大。
3、結論
本文提出了考慮螺旋角的銑削仿真模型,描述了殘余應力的模擬步驟以及穩定區殘余應力的獲取方法,對銑削工藝參數對表面殘余應力的影響規律進行分析。結論如下:
1) 銑削工藝引入表面殘余應力為壓應力,量級為 - 20~-50MPa,影響殘余應力深度為 0~100μm,并且隨著深度的增加,殘余壓應力逐漸減小,進而趨于 0。
2) 隨著主軸轉速的增加,表層殘余壓應力有減小趨勢,而對殘余壓力層的層深幾乎沒有影響。這是因為主軸轉速的增加時,刀具每齒單次切削時的速度變快,切削溫度升高,切削熱增加,因此熱效應引起的殘余拉應力占主要地位,表面殘余應力隨著主軸轉速的增加逐漸向拉應力轉換。
3) 隨著每轉進給量的增加,表面殘余壓應力總體呈現增大趨勢,并且殘余壓應力影響深度層增大。在較高的進給量情況下,材料去除增快,機械載荷引起的殘余應力起主導作用,此時增大進給量,“擠光效應” 增強,工件表面層壓應力增大。
需要指出的是,切削仿真模型的計算準確性受到多種因素綜合影響,包括材料本構模型、切屑斷裂準則、刀具幾何簡化、表面摩擦、冷卻效果、材料相變、刀具磨損等。本文采用的考慮螺旋角的二維切削模型中,相較于二維正交切削模型中的簡化處理,在刀尖角度簡化方面更貼近實際情況。而為精確獲取復雜環境下的切削殘余應力,仍需在材料本構模型、切屑形成與斷裂準則、表面摩擦行為、切削誘導材料相變機理等方面開展更深入的研究。
參考文獻
[1] IATA. Safety Overview [R]. Montreal, Canada: International air transport association, 2024.
[2] FAA. e-CFR 14 part 33, Airworthiness standards: aircraft engines [S]. Washington D.C., USA: FAA, 2009.
[3] FAA. Advisory Circular 33.75-1A: Guidance material for 14 CFR §33.75, safety analysis [R]. Washington D.C., USA: Federal Aviation Administration, 2007.
[4] FAA. Advisory Circular 33.75-1A with Change1: Guidance material for 14 CFR §33.75, safety analysis [R]. Washington D.C., USA: Federal Aviation Administration, 2015.
[5] National Transportation Safety Board. Powerplant Group Chairman’s Factual Report, NTSB No: ENG14IA028 [R]. Washington D.C.: National Transportation Safety Board, No: ENG14IA028, 2016.
[6] Japan Transport Safety Board. Aircraft accident investigation report: Korean airlines Co., LTD. HL7534, AA2018-5 [R]. Japan Transport Safety Board, 2018.
[7] FIELD M, KAHLES J F. The surface integrity of machined and groud high strength steels [R]. DMIC report 210: 54-57.
[8] GAO Y K. Improvement of fatigue property in 7050T7451 aluminum alloy by laser peening and shot peening [J]. Materials Science and Engineering A, 2011, 528: 3823-3828.
[9] JAVIDI A, RIEGER U, EICHLSEDER W. The effect of machining on the surface integrity and fatigue life [J]. International Journal of Fatigue, 2008, 30: 2050-2055.
[10] 杜東興。表面改性與完整性對鈦合金疲勞行為的影響 [D]. 西安:西北工業大學,2014. DU Dongxing. Effects of surface modification and integrity on fatigue behaviors of titanium alloy [D]. Xi’an: Northwestern Polytechnical University, 2014. (in Chinese)
[11] YAO Changfeng, WU Daoxia, JIN Qichao, et al. Influence of high-speed milling parameter on 3D surface topography and fatigue behavior of TB6 titanium alloy [J]. Transactions of Nonferrous Metals Society of China, 2013, 23 (3): 650-660.
[12] SMITH S, MELKOTE S N, LARA-CURZIO E, et al. Effect of surface integrity of hard turned AISI 52100 steel on fatigue performance [J]. Materials Science and Engineering: A, 2007, 459 (1-2): 337-346.
[13] 楊茂,陸山,潘容,等。噴丸殘余應力及夾雜影響小裂紋仿真概率模型 [J]. 航空動力學報,2023, 38 (4): 913-920. YANG Mao, LU Shan, PAN Rong, et al. Probabilistic model of small crack simulation considering shot peening residual stress and inclusion influence [J]. Journal of Aerospace Power, 2023, 38 (4): 913-920. (in Chinese)
[14] NOVOVIC D, DEWES R C, ASPINWALL D K, et al. The effect of machined topography and integrity on fatigue life [J]. International Journal of Machine Tools & Manufacture, 2004 (44): 125-134.
[15] 楊興宇,趙福星,耿中行。用殘余應力確定渦輪盤應變循環研究 [J]. 航空動力學報,2004, 19 (5): 614-618. YANG Xingyu, ZHAO Fuxing, GENG Zhongxing. A study on the maximal turbine disk strain cycle with residue stress [J]. Journal of Aerospace Power, 2004, 19 (5): 614-618. (in Chinese)
[16] 陳志君. LA103Z 鋰鎂合金構件銑削加工殘余應力研究 [D]. 北京:北京科技大學,2024. CHEN Zhijun. Research on residual stress during milling of LA103Z Mg-Li Alloy Part [D]. Beijing: University of Science and Technology Beijing, 2024. (in Chinese)
[17] WAN Zhenping, ZHU Y E, LIU Hongwei, et al. Microstructure evolution of adiabatic shear bands and mechanisms of saw-tooth chip formation in machining Ti6Al4V [J]. Materials Science and Engineering: A, 2012, 531: 155-163.
[18] MERCHANT M E. Mechanics of the metal cutting process. I. Orthogonal cutting and a type 2 chip [J]. Journal of applied physics, 1945, 16 (5): 267-275.
[19] SHAW M C. A quantized theory of strain hardening as applied to the cutting of metals [J]. Journal of Applied Physics, 1950, 21: 599-606.
[20] LEE E H, SHAFFER B W. The theory of plasticity applied to a problem of machining [J]. Journal of Applied Mechanics-transactions of the ASME, 1951, 18: 405-413.
[21] PALMER W B, OXLEY P L B. Mechanics of orthogonal machining [J]. Proceedings of the Institution of Mechanical Engineers, 1959, 173 (1): 623-654.
[22] OXLEY P L B, SHAW M C. Mechanics of machining: an analytical approach to assessing machinability [M]. Chichester, England: Ellis Horwood Linited, 1989.
[23] LI Binglin, WANG Xuelin, HU Yujin, et al. Analytical prediction of cutting forces in orthogonal cutting using unequal division shear-zone model [J]. The International Journal of Advanced Manufacturing Technology, 2011, 54 (5-8): 431-443.
[24] KLAMECKI B E. Incipient chip formation in metal cutting-a three dimension finite analysis [D]. Urbana: University of Illinois at Urbana-Champaign, 1973.
[25] USUI E, SHIRAKASHI T. Mechanics of machiningfrom descriptive to predictive theory [J]. On the art of cutting metals-75 Years Later, 1982: 13-35.
[26] IWATA K, OSAKADA K, TERASAKA Y. Process modeling of orthogonal cutting by the rigid-plastic finite element method [J]. Journal of Engineering Materials and Technology,1984,106 (2): 132-138.
[27] STRENKOWSKI J S, CARROLL J T. A finite element model of orthogonal metal cutting [J]. Journal of Engineering for Industry,1985,107 (4): 349-354.
[28] SHIH A J. Finite element simulation of orthogonal metal cutting [J]. Journal of Engineering for Industry,1995,117 (1): 84-93.
[29] SASAHARA H, OBIKAWA T, SHIRAKASHI T. FEM analysis of cutting sequence effect on mechanical characteristics in machined layer [J]. Journal of Materials Processing Tech., 1996, 62 (4): 448-453.
[30] 袁平。采用多刃銑刀的航空鋁合金高速加工過程的數值模擬與實驗研究 [D]. 浙江:浙江大學,2008. YUAN Ping. Simulation and experimental study on the high speed milling process for aerospace aluminum alloy with multi-flutes milling cutter [D]. Zhejiang: Zhejiang University, 2008. (in Chinese)
[31] 司璐。基于切削仿真技術的鈦合金薄壁件加工用整體式銑刀側刃參數設計 [D]. 哈爾濱:哈爾濱理工大學,2020. SI Lu. Parameters design of milling cutter for titanium alloy thin-wall part based on cutting simulation technology [D]. Harbin: Harbin University of Science and Technology, 2020. (in Chinese)
[32] 姜峰。不同冷卻潤滑條件 Ti6Al4V 高速加工機理研究 [D]. 山東:山東大學,2009. JIANG Feng. Study on Ti6Al4V high-speed machining mechanism under different cooling conditions [D]. Shandong: Shandong University, 2009. (in Chinese)
[33] 武永甫。航空鋁合金高速銑削表面殘余應力預測與實驗研究 [D]. 上海:上海交通大學,2013. WU Yongfu. Surface residual stress prediction and experimental research for high-speed milling of aerospace aluminum alloy [D]. Shanghai: Shanghai Jiao Tong University, 2013. (in Chinese)
[34] 肖珞瓊。基于等效刀具參數的 Cr12MoV 模具鋼銑削性能有限元分析 [D]. 湖南:湖南大學,2017. XIAO Luoqiong. Finite element analysis of milling performance of die steel Cr12MoV based on equivalent tool parameters [D]. Hunan: Hunan University, 2017. (in Chinese)
[35] SAOUBI R M, OUTEIRO J C, CHANGEUX B, et al. Residual stress analysis in orthogonal machining of standard and resulfurized AISI 316L steels [J]. Journal of Materials Processing Technology, 1999, 96 (1-3): 225-233.
[36] GRISSA R, ZEMZEMI F, and FATHALLAH R. Three approaches for modeling residual stresses induced by orthogonal cutting of AISI316L [J]. International Journal of Mechanical Sciences, 2018, 135: 253-260.
[37] CHENG Wenyu, OUTEIRO J C. Modelling orthogonal cutting of Ti6Al4V titanium alloy using a constitutive model considering the state of stress [J]. The International Journal of Advanced Manufacturing Technology, 2022, 119: 4329-4347.
[38] 吳遠晨。鈦合金 TC4 銑削加工刀具磨損的有限元研究 [D]. 山東:山東大學,2014. WU Yuanchen. FEM simulation of milling tool wear for titanium alloys TC4 [D]. Shandong: Shandong University, 2014. (in Chinese)
[39] 竇雪平。考慮已加工表面殘余應力的銑削過程優化 [D]. 哈爾濱:哈爾濱理工大學,2021. DOU Xueping. Milling process optimization consideration residual stress of machined surface [D]. Harbin: Harbin University of Science and Technology, 2021. (in Chinese)
[40] RICE J R, TRACEY D M. On the ductile enlargement of voids in triaxial stress fields [J]. Journal of the Mechanics and Physics of Solids, 1969, 17 (3): 201-217.
[41] COCKCROFT M G, LATHAM D J. Ductility and the workability of metals [J]. Journal of the Institute of Metals, 1968, 96: 33-39.
[42] Deform 2D version 14.1 User’s Manual, 2024.
[43] OYANE M, SATO T, OKIMOTO K, et al. Criteria for ductile fracture and their applications [J]. Journal of Mechanical Working Technology, 1980, 4 (1): 65-81.
[44] BAI Wei, SUN Ronglei, LEOPOLD J, et al. Microstructural evolution of Ti6Al4V in ultrasonically assisted cutting: Numerical modelling and experimental analysis [J]. Ultrasonics, 2017, 78: 70-82.
[45] UMBRELLO D. Finite element simulation of conventional and high speed machining of Ti6Al4V alloy [J]. Journal of Materials Processing Technology, 2008, 196: 79-87.
[46] BERGER S, BROCK G, BIERMANN D. Simulative design of constraints for targeted restriction of chip thickness deviations when machining titanium alloy Ti6Al4V [C]. 18the CIRP Conference on Modeling of Machining Operations, 2021, 102: 86-90.
[47] 崔玉龍。考慮殘余應力的球頭銑刀銑削鈦合金集成仿真優化研究 [D]. 哈爾濱:哈爾濱理工大學,2020. CUI Yulong. Research on integrated simulation and optimization of ball-end milling cutter milling titanium alloy considering residual stress [D]. Harbin: Harbin University of Science and Technology, 2020. (in Chinese)
[48] ZHOU Huimin, LIU Junbo, BAO Shaochen, et al. Probabilistic Risk Assessment Method Considering Machining-induced Random Residual Stress [J]. International Journal of Mechanical Sciences, 2025, 285: 1-17.
(注,原文標題:銑削工藝對鈦合金輪盤表面殘余應力影響規律)
相關鏈接